LAS Lossy Audio Spotter

FLAC is supposed to be a lossless codec. Actually it is, but the source might not be. Stupid people, or worse, evil ones, might pretend to release a lossless copy of a song while they've only transcoded some lossy MP3 to FLAC files.

This post explains the various steps I followed to write LAS, a tool able to give a guess about the original quality of the source. It is not 100% efficient, but it works for most of the cases. There are certainly better algorithms out there, this is just my simple attempt to solve the issue.

Observation

Let's take a random lossless FLAC sample, and transcode it to a MP3 in CBR:

% ffmpeg -i lossless.flac -ab 192k lossy.mp3

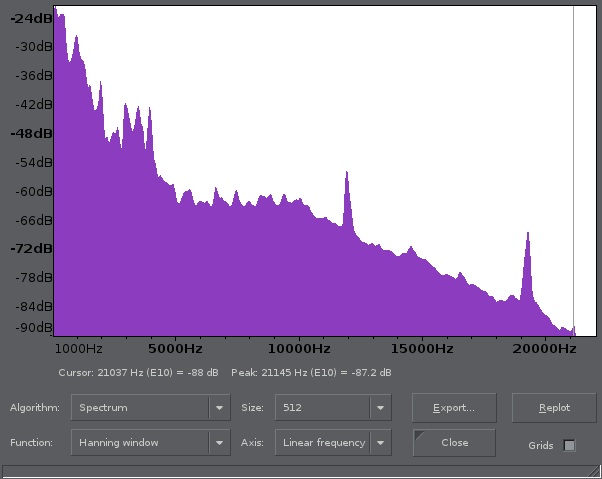
So what could we do to detect the fraud without the original copy? Well, we can do a simple observation in Audacity; these are the respective spectrum histograms (Analyze → Plot Spectrum):

Here is the original:

And the MP3:

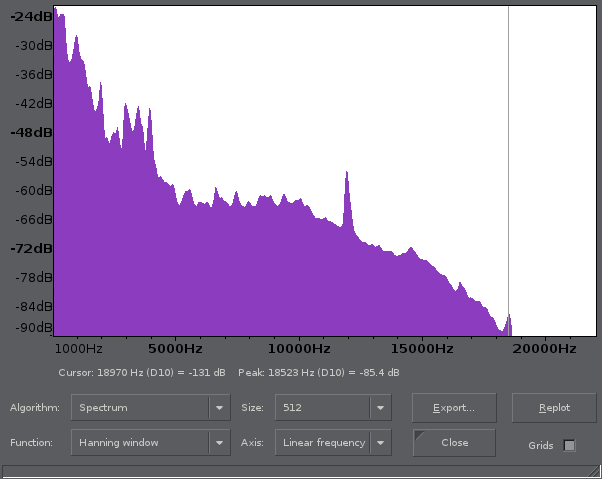
It is obvious with those histograms that higher frequencies are never reached, so this is where we will try to operate.

The same scheme is observable with CBR 320k (highest available bit rate), and high/low VBR encodes; the no magnitude's land is just found at different frequencies.

We will start by reproducing those histograms and then analyze them.

How to proceed

This section will present the content of the main struct and will resume the execution flow.

First, we will use FFmpeg to decode the audio (because it's great, and it also implements FFT stuff). We will keep in the structure a pointer to the codec (will be needed at least to decode the audio packets, and access the number of channels):

AVCodecContext *codec;

The decoded data frame will be stored in a buffer:

uint8_t *audio_buf;

The samples (amplitudes) will be extracted from audio_buf in an appropriate buffer of 16-signed-bits precision. Note that we can not use audio_buf directly because samples must have a specific size before applying the Fast Fourier Transform, and audio_buf length is undefined. So the samples will be stored in:

int16_t *samples;

...and its size in bytes stored in:

int samples_bsize;

The amount of samples filled (in bytes) after decoding each packet is stored in:

int filled;

It will be used to know when to send the samples to the process function (flush).

We will also need some pointers for the FFT. Since we will apply a Real Discrete Fourier Transform, we need the appropriate context (still using the FFmpeg API):

RDFTContext *rdft;

With the following buffer as input (samples will be stored in that buffer before being transformed):

FFTSample *rdft_data;

This FFT will transform FFT_WINSIZE samples to FFT_WINSIZE/2 + 1 complex bins. FFT_WINSIZE is the size of each window; it's the N you know when doing FFT. And we will need to keep a counter of those processed windows, so we can average them later:

int win_count;

The magnitude will be tracked in that last buffer:

float fft[FFT_WINSIZE/2 + 1];

Given all those parameters, and window size of 512B, we will have:

#define FFT_NBITS   9
#define FFT_WINSIZE (1<<FFT_NBITS)

struct las {
    AVCodecContext *codec;
    uint8_t *audio_buf;
    int16_t *samples;
    int samples_bsize;
    int filled;
    RDFTContext *rdft;
    FFTSample *rdft_data;
    int win_count;
    float fft[FFT_WINSIZE/2 + 1];
};

Decoding the audio

Before decoding the audio file, let's initialize FFmpeg, load the file, find the first audio stream, open the codec, and check for the number of audio channels (we will only support up to 2 channels):

/* FFmpeg init */
av_register_all();
AVFormatContext *fmt_ctx = NULL;
if (avformat_open_input(&fmt_ctx, av[1], NULL, NULL) ||
    av_find_stream_info(fmt_ctx) < 0)
    errx(1, "unable to load %s", av[1]);
int stream_id = -1;
for (unsigned i = 0; i < fmt_ctx->nb_streams; i++) {
    if (fmt_ctx->streams[i]->codec->codec_type == AVMEDIA_TYPE_AUDIO) {
        stream_id = i;
        break;
    }
}
if (stream_id == -1)
    errx(1, "no audio stream found");
ctx.codec = fmt_ctx->streams[stream_id]->codec;
AVCodec *adec = avcodec_find_decoder(ctx.codec->codec_id);
if (!adec)
    errx(1, "unsupported codec");
avcodec_open(ctx.codec, adec);
if (ctx.codec->channels != 1 && ctx.codec->channels != 2)
    errx(1, "unsupported number of channels (%d)", ctx.codec->channels);

Now, let's see our own stuff:

/* LAS init */
precalc_hann();
ctx.samples_bsize = FFT_WINSIZE * ctx.codec->channels * sizeof(*ctx.samples);
ctx.samples       = av_malloc(ctx.samples_bsize);
ctx.rdft          = av_rdft_init(FFT_NBITS, DFT_R2C);
ctx.rdft_data     = av_malloc(FFT_WINSIZE * sizeof(*ctx.rdft_data));
ctx.audio_buf     = av_malloc(AVCODEC_MAX_AUDIO_FRAME_SIZE);

A few notes are needed here. precalc_hann() is just a small function used to initialize the Hann function (which is needed to get smooth FFT results) LUT:

static float hann[FFT_WINSIZE];

static void precalc_hann(void)
{
    for (int i = 0; i < FFT_WINSIZE; i++)
        hann[i] = .5f * (1 - cos(2*M_PI*i / (FFT_WINSIZE-1)));
}

The samples size (in bytes) is pretty straightforward; we need FFT_WINSIZE samples, times the number of channels (which will be downmix to mono channel later) times the size of one sample.

The FFmpeg RDFT is only able to perform FFT with buffer of size being a power of two, and this is expressed with a number of bits FFT_NBITS (1<<2=4, 1<<3=8, 1<<4=16, etc.). DFT_R2C means Discrete Fourier Transform from Real numbers to Complex numbers. It will transform a window of FFT_WINSIZE samples: rdft_data.

Last one is the audio_buf mentionned above already, which needs a size of AVCODEC_MAX_AUDIO_FRAME_SIZE. Note that we avoid stack allocation and prefer av_malloc() because of some data alignment requirements (FFmpeg API) and performance reasons.

We can now read the frames and process the audio packets:

AVPacket pkt;
while (av_read_frame(fmt_ctx, &pkt) >= 0)
    if (pkt.stream_index == stream_id && process_audio_pkt(&ctx, &pkt) < 0)
        warnx("error while processing audio packet");

Since the buffer might have some information left, we pad the buffer with zeros (we need FFT_WINSIZE samples, and the buffer have garbage/old data at the end) and flush it:

if (ctx.filled) { // flush buffer
    memset((uint8_t*)ctx.samples + ctx.filled, 0, ctx.samples_bsize - ctx.filled);
    process_samples(&ctx);
}

Here is the process_audio_pkt() verbatim:

static int process_audio_pkt(struct las *c, AVPacket *pkt)
{
    while (pkt->size > 0) {
        uint8_t *data = c->audio_buf;
        int data_size = AVCODEC_MAX_AUDIO_FRAME_SIZE;
        int len       = avcodec_decode_audio3(c->codec, (int16_t*)data, &data_size, pkt);
        if (len < 0) {
            pkt->size = 0;
            return -1;
        }
        pkt->data += len;
        pkt->size -= len;
        while (data_size > 0) {
            int needed = c->samples_bsize - c->filled; // in bytes
            int ncpy   = data_size >= needed ? needed : data_size;
            memcpy((uint8_t*)c->samples + c->filled, data, ncpy);
            c->filled += ncpy;
            if (c->filled != c->samples_bsize)
                break;
            process_samples(c);
            data      += ncpy;
            data_size -= ncpy;
        }
    }
    return 0;
}

It will basically decode the packet, fill our samples buffer, and call process_samples() when a buffer is ready.

Processing the audio data

Alright, now we are in process_samples() and have FFT_WINSIZE samples available for processing.

static void process_samples(struct las *c)
{
    c->win_count++;
    c->filled = 0;

So first, we need to downmix (to mono-channel), resample (from signed 16-bits integer to [0;1] floats), and apply the Hann window on the samples:

// Resample (int16_t to float), downmix if necessary and apply hann window
int16_t *s16 = c->samples;
switch (c->codec->channels) {
case 2:
    for (int i = 0; i < FFT_WINSIZE; i++)
        c->rdft_data[i] = (s16[i*2] + s16[i*2+1]) / (2*32768.f) * hann[i];
    break;
case 1:
    for (int i = 0; i < FFT_WINSIZE; i++)
        c->rdft_data[i] = s16[i] / 32768.f * hann[i];
    break;
}

And then apply FFT, compute the magnitude (not normalized, and without the square root) for each sample:

    // FFT
#define FFT_ASSIGN_VALUES(i, re, im) c->fft[i] += re*re + im*im
    float *bin = c->rdft_data;
    av_rdft_calc(c->rdft, bin);
    for (int i = 1; i < FFT_WINSIZE/2; i++)
        FFT_ASSIGN_VALUES(i, bin[i*2], bin[i*2+1]);
    FFT_ASSIGN_VALUES(0,             bin[0], 0);
    FFT_ASSIGN_VALUES(FFT_WINSIZE/2, bin[1], 0);
}

av_rdft_calc() processes FFT_WINSIZE samples and gives FFT_WINSIZE/2 + 1 bins. How is that possible in the input buffer since we have two bins for one sample?

Logically we would need a buffer of (FFT_WINSIZE/2+1)*2 = FFT_WINSIZE+2 bytes, and not FFT_WINSIZE. But actually, the first and last bins are real numbers, which means their imaginary parts are always zero: so the buffer is composed of couples of real and imaginary floats except for the two first ones which are the real parts of the first and last bins. The last two lines of code are for these extractions.

Display the histogram

It's time to check out the histogram. fft field now contains the sum of all the magnitudes for each frequency range. We assume the input is encoded at 44100Hz, so FFT_WINSIZE/2+1 entries in fft will correspond to the magnitudes from 0 to 44100/2=22050Hz.

In order to get a graph similar to what we got in the first place with audacity, we first have to average the values (divide each entry by the windows count), and scale it with FFT_WINSIZE. And then, we need to convert the magnitude in dB. Since there was no square root used on the magnitude, we won't use 20 * log10(x) but 10 * log10(x).

Here is the code used to print the magnitude of each frequencies to be piped to Gnuplot:

printf("set terminal png font tiny size 300,200\n"
       "set style data boxes\n"
       "set style fill solid\n"
       "set xrange [0:%f]\n"
       "set yrange [-120:0]\n"
       "set xlabel 'Frequency (kHz)'\n"
       "set ylabel 'Log magnitude (dB)'\n"
       "plot '-' using ($0/%d.*%f):1 notitle\n",
       44.1f/2.f, FFT_WINSIZE, 44.1f);
for (i = 0; i < sizeof(ctx.fft)/sizeof(*ctx.fft); i++) {
    float x = ctx.fft[i] / ctx.win_count / FFT_WINSIZE;
    ctx.fft[i] = 10 * log10(x ? x : -1e20);
    printf("%f\n", ctx.fft[i]);
}

Exploit the results

And now the fun. How can we figure out the higher frequency from the graph? Well, let's first do a pretty simple heuristic:

/* Find higher frequency used */
unsigned last = sizeof(ctx.fft)/sizeof(*ctx.fft) - 1;
for (i = last - 1; i > 0; i--)
    if (fabsf(ctx.fft[i] - ctx.fft[last])  > 1.5f ||
        fabsf(ctx.fft[i] - ctx.fft[i + 1]) > 3.f)
        break;

We take the last entry and check from the end (higher frequency) to the beginning (lower frequency) trying to detect a fluctuation. The error ranges of 1.5f and 3.f are chosen by trial and error, and seemed pretty efficient here with my samples.

I also added a second check: the huge fall lookup. The previous check does not always work out, and we need to look for something else. This second heuristic seems to cover most of the exceptions:

    /* Try to detect huge falls too */
#define THRESHOLD_FALL 5
    for (unsigned n = i - THRESHOLD_FALL; n; n--) {
        if (ctx.fft[n] - ctx.fft[n + THRESHOLD_FALL] > 25.f) {
            i = n;
            break;
        }
    }

After computing the higher frequency from i, we can check if it's "high enough" to be considered lossless:

/* Report lossy/lossless estimation in a Gnuplot comment */
int hfreq = i * 44100 / FFT_WINSIZE;
printf("# higher freq=%dHz → %s\n", hfreq, hfreq < 21000 ? "lossy" : "lossless");

Again, the 21000Hz value was obtained by trial and error.

Testing

The complete source is available on Github and includes a analyze.sh script which takes files and directories as argument, scans all the FLAC in it, and generates a all-in-one report.html page to summarize all the results:

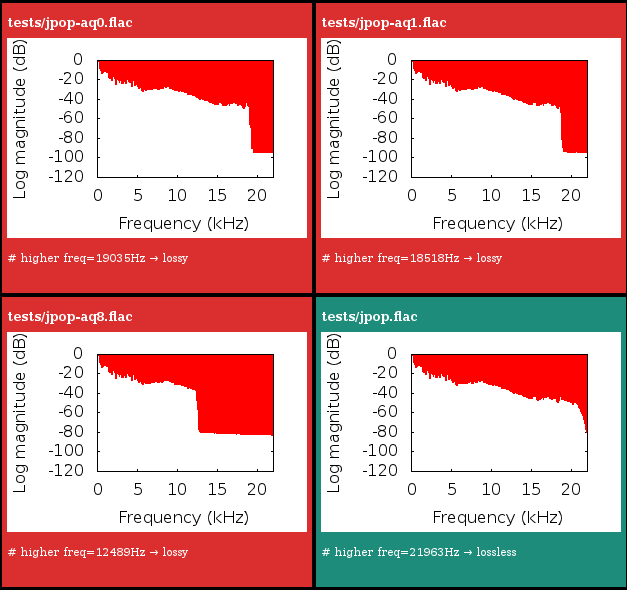
I tested the code with a few FLAC from different musical genres re-encoded with various high and low VBR and CBR MP3 profiles, and re-transcoded to FLAC. Here is the small script I used to generate those samples (can be pretty long to execute):

#!/bin/sh

for f in *.flac; do
    name=${f%.flac}
    for aq in 0 1 2 6 8;      do ffmpeg -i $f -aq ${aq}  ${name}-aq${aq}.mp3; done
    for ab in 64 128 192 320; do ffmpeg -i $f -ab ${ab}k ${name}-${ab}k.mp3;  done
done
for mp3 in *.mp3; do
    ffmpeg -i $mp3 ${mp3%.mp3}.flac;
done
rm -f *.mp3

Have no fear of perfection - you'll never reach it. S. Dali

The project is not mature enough, we might be able to do something simpler (I guess we can get rid of the dB conversion completely for instance), and more efficient (another algorithm, better chosen coefficient, etc.), but right now it seems to work pretty fine in all my tests.

Also, I did not test at all with other codecs like Vorbis, so there is certainly some path to improvement here.

I don't know if there are already stuff out there related to this research. If you have something on that matter, feel free to send it. Also, I'm all open for samples, better values, algorithms, various comments, etc.