Perfecting anti-aliasing on signed distance functions

Doing anti-aliasing on SDF is not as straightforward as it seems. Most of the time, we see people use a smoothstep with hardcoded constants, sometimes with screen space information, sometimes cryptic or convoluted formulas. Even if SDFs have the perfect mathematical properties needed for a clean anti-aliasing, the whole issue has a scope larger than it appears at first glance. And even when trivial solutions exist, it's not always clear why they are a good fit. Let's study that together.

SDF

The article assumes that you are at least a bit familiar with what an SDF is, but if I had to provide a quick and informal definition, I would say something like:

"It's a function (or lookup-table of said function, usually stored in a texture) which returns the signed distance from the specified coordinates to a given shape, where the sign indicates whether you're inside or outside the shape."

A common visualization of it looks like this:

The distance is fancily colored here for illustrative purpose, and the shape is animated to see how it affects the field.

Another way of seeing it is to switch to a 3D view:

For the sign interpretation, here we're using the convention positive inside and negative outside, as seen for example on the Wikipedia illustration. But this is not always the case, for example, Inigo prefers the opposite: negative inside and positive outside. I personally find the Wikipedia convention to be more intuitive and easy to work with, but that's a matter of preferences so we'll figure out the formulas for both models. Switching from one to the other is just a sign swap, but it's important to know what we are working with.

Linear ramp

A properly crafted SDF has a gradient of length 1, meaning the slope is either going up or down, but always at the same constant rate of 1:

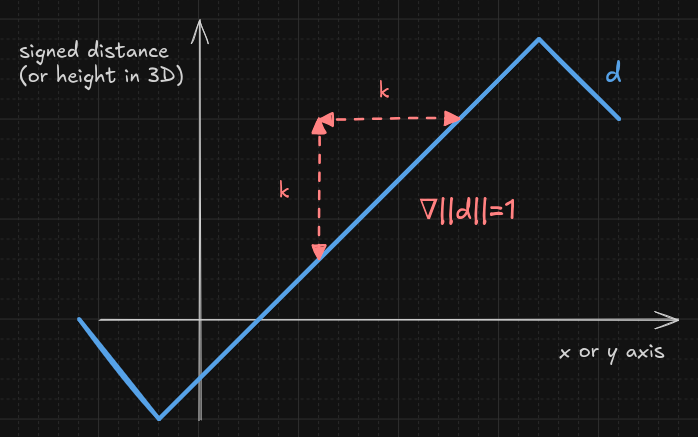
This is an important property since anti-aliasing is all about transitioning smoothly toward (or away from) the shape. For our first attempt at anti-aliasing we will simply follow that ramp and make a straight transition.

Once again, we are going to rely on linear, one of the most useful math formulas:

float linear(float a, float b, float x) { return (x-a)/(b-a); }

And more specifically we will need its saturated version linearstep:

float linearstep(float a, float b, float x) { return clamp(linear(a,b,x), 0.0, 1.0); }

This is the same as the well-known smoothstep, except it's a straight line when transitioning from a to b.

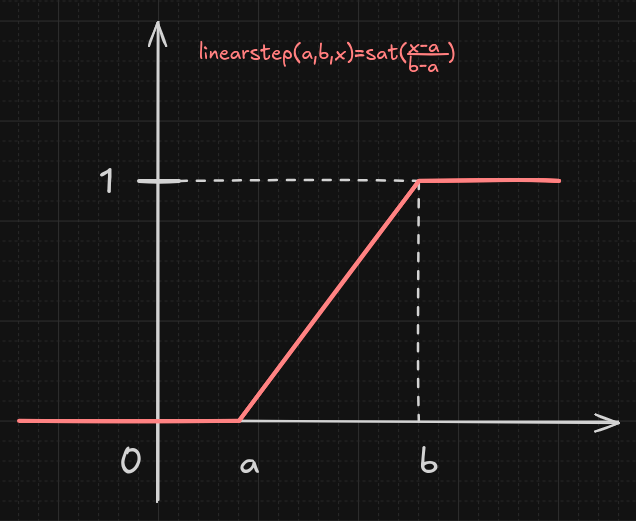
The length of our ramp (the transition zone between a and b) is going to be arbitrary at first, we will call it w (for "width"). It's our diffuse, or blur parameter if you prefer. The height h we are looking for corresponds to the opacity of our shape.

Given a positive inside and negative outside SDF, we will start with the transition centered around the boundary between the shape and its outside.

You might be confused about the relationship between the distance and the transition zone (diffuse width w). The following diagram may help clarifying why:

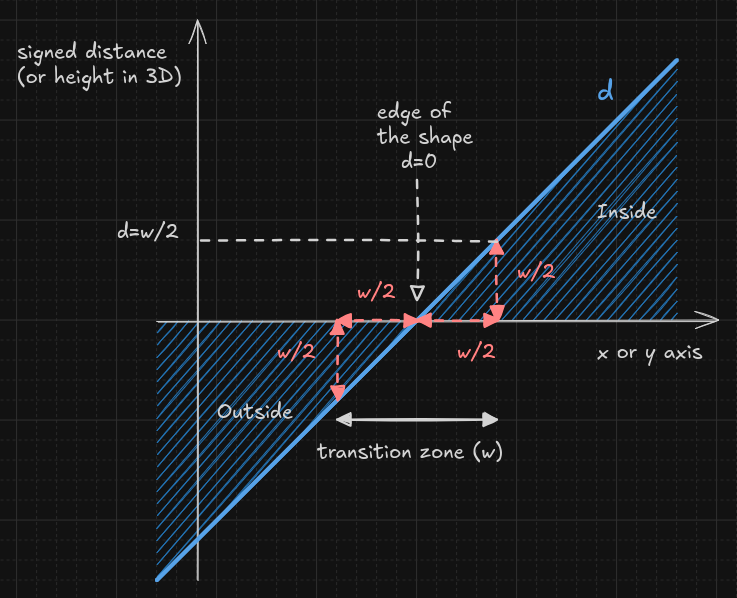
Remember, the gradient of an SDF is supposed to have a length of 1. This means there is a direct match between the height of the signed distance (y-axis on the figure), and the spacial distance traveled (x-axis on the figure).

The previous figure shows that for a centered transition, when the distance d is within [-w/2,w/2], it represents a transition width of size w around the edge, so we want it to be mapped to an opacity within [0,1]. This can be expressed with:

float h = linearstep(-w/2.0, w/2.0, d);

Which can be unrolled and simplified into the following tiny form:

float h = clamp(0.5 + d/w, 0.0, 1.0);

We can also decide to make the transition on the outside or the inside boundary of the shape:

float h_in  = linearstep(0.0, w, d);  // or simply clamp(    d/w, 0.0, 1.0);
float h_out = linearstep(-w, 0.0, d); // or simply clamp(1.0+d/w, 0.0, 1.0);

And we can be creative and have a cursor indicating where we are on the border. If we give k=0 for inside, k=0.5 for centered and k=1 for outside:

float h = clamp(k + d/w, 0.0, 1.0);

For the negative inside and positive outside SDF, we simply swap the sign:

float h = clamp(k - d/w, 0.0, 1.0);

Any of these one-liners is all we need to have AA for our shape, but the question of what value to use for the ramp width w arises.

Pixel size

The difference between a blur and anti-aliasing is simply the width value. With AA, it's the size of a "pixel", and with a blur it's typically a user input or an arbitrarily large value.

If we are in 2D and have access to the pixel resolution, we can use it to get the pixel size. Note that this is closely tied to the coordinate space we use to calculate the SDF.

For example, let's say we have a canvas for which we don't know the aspect ratio, we can calculate the screen coordinates like this:

vec2 p = (2.0*gl_FragCoord.xy - resolution) / min(resolution.x, resolution.y);

This will give us a p value within [-1,1] on the shortest axis (the y-axis in landscape mode) and preserve a squared aspect ratio. That means the shortest axis will have an amplitude of 2, which means the number of pixel on that axis correspond to 2 units. As a result, the unit-width that will be used for the signed distance can be obtained with:

float w = 2.0 / min(resolution.x, resolution.y);

Remember that this is true only if the position p we use for the SDF is in that range. Basically, we have to adjust this formula to the coordinate space we are using.

The same with a x10 resolution to better see the AA:

3D and numerical derivatives

But sometimes we might not have access to the resolution, or we may want to map that 2D SDF onto a plane in 3D or some other transformation. For example, a decal or a text on the wall in a video game. In that later case, if we were to use the screen resolution, it would lead to inconsistent anti-aliasing:

We can see that, when put in perspective, the edge in the back gets way too sharp while the edge in the front becomes a bit too blurry. Fortunately, there is a magic trick we can use, the numerical derivatives:

float w = fwidth(d);

Now we magically have a smooth pixel-wise anti-aliasing, no matter the perspective. What is this sorcery? 🧙

fwidth calculate the rate of change of a given variable using fragment-based numerical derivatives. Mathematically this is a L1-norm (also known as Taxicab or Manhattan norm) defined as: abs(dFdx(x)) + abs(dFdy(x)).

But how the hell is this providing a good pixel width estimate?

Let's see the simple case where we want observe the rate of change of one variable across one axis. For example, dFdx(px) where px is the pixel coordinate: int px = gl_FragCoord.x. We will have dFdx(px)=1. Why? Because x changes at a constant rate of 1 (exactly like our SDF) from one pixel to another. If we remap px to a value between [-1,1] using p=px/W*2.0-1.0 (where W is the number of pixels on the x axis), we can follow derivation rules and end up with: dFdx(p)=2.0/W. This matches with our initial pixel size computation w in our previous section.

Now when 3D and perspective distortions are involved, this still holds and you may be wondering why. The intuitive answer is that fwidth(d) is the rate of change of the signed distance as seen from the flat pixel screen perspective. In 3D view, in the back of the shape, the distance d changes sharply from one pixel to another (meaning fwidth(d) will be high), while in the front it's way smoother (meaning fwidth(d) will be low). So this numerical derivative is used to scale the distance back to a transition that works smoothly from the 2D pixel point of view.

Numerical derivatives refinement

Instead of fwidth, we could also use the L2-norm (also known as euclidean distance):

float w = length(vec2(dFdx(d), dFdy(d)));

This is more expensive than fwidth, but it can be considered as an alternative. The AA will be slightly different but it's hard to say which one really is better than the other:

Straight vs smooth(er) ramp

Instead of a linearstep() some people like to use smoothstep(). The main reason is probably because smoothstep() is available in builtin while linearstep() isn't. But is it a better choice?

Intuitively, to me at least, it makes perfect sense for the alpha value to follow a linear ramp. A few weeks ago I would have adamantly argued that it's actually a faster and more logical choice than its curved version smoothstep.

Well... I did some tests. With a large diffuse, here is what it looks like with a linear ramp:

It looks like there is a brighter highlight around the border (before the fall-off), doesn't it? Well, it's an illusion, it's just our brain noticing the discontinuity and telling us about it.

With a smoothstep things get better:

I wasn't expecting that, so I stand corrected: smoothstep is actually a better choice. It's also builtin, so we won't need to define our own function.

Of course, one may prefer an even smoother curve, for example smootherstep() using the quintic curve instead of the hermite:

float smootherstep(float a, float b, float x) {
    float t = linearstep(a, b, x);
    return ((6.0*t-15.0)*t+10.0)*t*t*t; // quintic
}

Color space

When we have our anti-aliasing value, it's pretty much done. But we still have the question on how to use it. My previous examples were in black and white, but in many cases we need blending between colors. The question of how to blend is probably the most tricky of all, and my previous article was entirely dedicated to this particular issue.

In all the examples from this page, I've been using the OkLab blending because "it's perfect". But the reality is likely to force you to use a simple linear blending. For anti-aliasing, it's honestly just fine, the illusion still works out, but if you're trying to blur I would advise you against it and switch to a better colorspace like OkLab whenever possible.

See here how, because of how the human perception works, the linear blending does feel "bobby" and too large compared to OkLab:

Summary

Given all these tools we can combine them according to our needs and preferences. As closing words, let me propose a few reference examples:

A "good enough" centered linear ramp working in 2D or 3D

vec2 p = (2.0*gl_FragCoord.xy - resolution) / min(resolution.x, resolution.y);
float d = sdWP(p, ...); // signed distance, positive inside, negative outside SDF (Wikipedia style)
float h = clamp(0.5 + d/fwidth(d), 0.0, 1.0);
vec3 c = mix(c0, c1, h); // this assumes c0 and c1 colors are in linear space

A smooth user blur working in 2D only

float r = min(resolution.x, resolution.y);
vec2 p = (2.0*gl_FragCoord.xy - resolution) / r;
float w = max(u_blur, 2.0/r); // blur should not be smaller than unit size
float d = sdIQ(p, ...); // signed distance, negative inside, positive outside SDF (iQuilez style)
float h = smoothstep(-w/2.0, w/2.0, -d); // smooth centered blur
vec3 c = mix(c0, c1, h); // this assumes c0 and c1 colors are in linear space

An outer anti-aliasing with a more refined unit width estimation

vec2 p = (2.0*gl_FragCoord.xy - resolution) / min(resolution.x, resolution.y);
float d = sdWP(p, ...); // signed distance, positive inside, negative outside SDF (Wikipedia style)
float w = length(vec2(dFdx(d),dFdy(d))); // L2-norm width estimation
float h = smoothstep(-w, 0.0, d); // smooth outer AA
vec3 c = mix(c0, c1, h); // this assumes c0 and c1 colors are in linear space

Anti-aliasing SDFs can be beautifully simple, and now we also understand better the magic behind. ✨