For reasons I'll explain in a future write-up, I needed to make use of a perceptually uniform color space in some computer vision code. OkLab from Björn Ottosson was a great candidate given how simple the implementation is.

But there is a plot twist: I needed the code to be deterministic for the tests to be portable across a large variety of architecture, systems, and configurations. Several solutions were offered to me, including reworking the test framework to support a difference mechanism with threshold, but having done that in another project I can confidently say that it's not trivial (when not downright impossible in certain cases). Another approach would have been to hardcode the libc math functions, but even then I wasn't confident the floating point arithmetic would determinism would be guaranteed in all cases.
So I ended up choosing to port the code to integer arithmetic. I'm sure many people would disagree with that approach, but:
- Code determinism is guaranteed
- Not all FPU are that efficient, typically on embedded
- it can now be used in the kernel; while this is far-fetched for OkLab (though maybe someone needs some color management in v4l2 or something), sRGB transforms might have their use cases
- It's a learning experience which can be re-used in other circumstances
- Working on the integer arithmetic versions unlocked various optimizations for the normal case
Note
I'm following Björn Ottosson will to have OkLab code in the public domain as well as under MIT license, so this "dual licensing" applies to all the code presented in this article.
Warning
The integer arithmetic in this write-up can only work if your language behaves the same as C99 (or more recent) with regard to integer division. See this previous article on integer division for more information.
Quick summary of uniform colorspaces
For those unfamiliar with color management, one of the main benefit of a uniform colorspace like OkLab is that the euclidean distance between two colors is directly correlated with the human perception of these colors.
More concretely, if we want to evaluate the distance between the RGB triplets (R_0,G_0,B_0) and (R_1,G_1,B_1), one may naively compute the euclidean distance \sqrt{(R_0-R_1)^2+(G_0-G_1)^2+(B_0-B_1)^2}. Unfortunately, even if the RGB is gamma expanded into linear values, the computed distance will actually be pretty far from reflecting how the human eye perceive this difference. It typically isn't going to be consistent when applied to another pair of colors.
With OkLab (and many other uniform colorspaces), the colors are also
identified with 3D coordinates, but instead of (R,G,B) we call them
(L,a,b) (which is an entirely different 3D space). In that space
\sqrt{(L_0-L_1)^2+(a_0-a_1)^2+(b_0-b_1)^2} (called \Delta E, or Delta-E)
is expected to be aligned with human perception of color differences.
Of course, this is just one model, and it doesn't take into account many parameters. For instance, the perception of a color depends a lot on the surrounding colors. Still, these models are much better than working with RGB triplets, which don't make much sense visually speaking.
Reference code / diagram
In this study case, We will be focusing on the transform that goes from sRGB to OkLab, and back again into sRGB. Only the first part is interesting if we want the color distance, but sometimes we also want to alter a color uniformly and thus we need the 2nd part as well to reconstruct an sRGB color from it.
We are only considering the sRGB input and output for simplicity, which means we will be inlining the sRGB color transfer in the pipeline. If you're not familiar with gamma compression, there are many resources about it on the Internet which you may want to look into first.
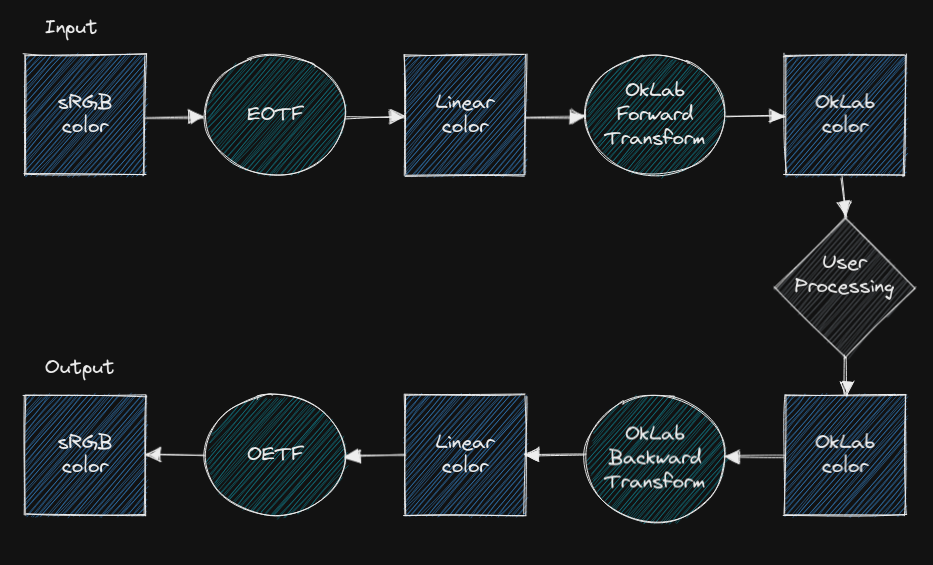
And the corresponding code (of the 4 circles in the diagram) we will be porting:
struct Lab { float L, a, b; }
uint8_t linear_f32_to_srgb_u8(float x)
{
if (x <= 0.0) {
return 0;
} else if (x >= 1.0) {
return 0xff;
} else {
const float v = x < 0.0031308f ? x*12.92f : 1.055f*powf(x, 1.f/2.4f) - 0.055f;
return lrintf(v * 255.f);
}
}
float srgb_u8_to_linear_f32(uint8_t x)
{
const float v = x / 255.f;
return v < 0.04045f ? v/12.92f : powf((v+0.055f)/1.055f, 2.4f);
}
struct Lab srgb_u8_to_oklab_f32(uint32_t srgb)
{
const float r = srgb_u8_to_linear_f32(srgb >> 16 & 0xff);
const float g = srgb_u8_to_linear_f32(srgb >> 8 & 0xff);
const float b = srgb_u8_to_linear_f32(srgb & 0xff);
const float l = 0.4122214708f * r + 0.5363325363f * g + 0.0514459929f * b;
const float m = 0.2119034982f * r + 0.6806995451f * g + 0.1073969566f * b;
const float s = 0.0883024619f * r + 0.2817188376f * g + 0.6299787005f * b;
const float l_ = cbrtf(l);
const float m_ = cbrtf(m);
const float s_ = cbrtf(s);
const struct Lab ret = {
.L = 0.2104542553f * l_ + 0.7936177850f * m_ - 0.0040720468f * s_,
.a = 1.9779984951f * l_ - 2.4285922050f * m_ + 0.4505937099f * s_,
.b = 0.0259040371f * l_ + 0.7827717662f * m_ - 0.8086757660f * s_,
};
return ret;
}
uint32_t oklab_f32_to_srgb_u8(struct Lab c)
{
const float l_ = c.L + 0.3963377774f * c.a + 0.2158037573f * c.b;
const float m_ = c.L - 0.1055613458f * c.a - 0.0638541728f * c.b;
const float s_ = c.L - 0.0894841775f * c.a - 1.2914855480f * c.b;
const float l = l_*l_*l_;
const float m = m_*m_*m_;
const float s = s_*s_*s_;
const uint8_t r = linear_f32_to_srgb_u8(+4.0767416621f * l - 3.3077115913f * m + 0.2309699292f * s);
const uint8_t g = linear_f32_to_srgb_u8(-1.2684380046f * l + 2.6097574011f * m - 0.3413193965f * s);
const uint8_t b = linear_f32_to_srgb_u8(-0.0041960863f * l - 0.7034186147f * m + 1.7076147010f * s);
return r<<16 | g<<8 | b;
}
sRGB to Linear
The first step is converting the sRGB color to linear values. That sRGB transfer function can be intimidating, but it's pretty much a simple power function:
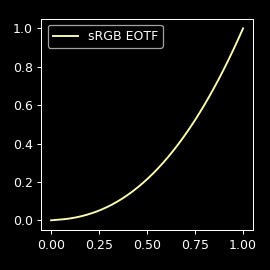
The input is 8-bit ([0x00,0xff] for each of the 3 channels) which means we
can use a simple 256 values lookup table containing the precomputed resulting
linear values. Note that we can already do that with the reference code with a
table remapping the 8-bit index into a float value.
For our integer version we need to pick an arbitrary precision for the linear
representation. 8-bit is not going to be enough precision, so
we're going to pick the next power of two to be space efficient: 16-bit. We
will be using the constant K=(1<<16)-1=0xffff to refer to this scale.
Alternatively we could rely on a fixed point mapping (an integer for the decimal part and another integer for the fractional part), but in our case pretty much everything is normalized so the decimal part doesn't really matter.
/**
* Table mapping formula:
* f(x) = x < 0.04045 ? x/12.92 : ((x+0.055)/1.055)^2.4 (sRGB EOTF)
* Where x is the normalized index in the table and f(x) the value in the table.
* f(x) is remapped to [0,K] and rounded.
*/
static const uint16_t srgb2linear[256] = {
0x0000, 0x0014, 0x0028, 0x003c, 0x0050, 0x0063, 0x0077, 0x008b,
0x009f, 0x00b3, 0x00c7, 0x00db, 0x00f1, 0x0108, 0x0120, 0x0139,
0x0154, 0x016f, 0x018c, 0x01ab, 0x01ca, 0x01eb, 0x020e, 0x0232,
0x0257, 0x027d, 0x02a5, 0x02ce, 0x02f9, 0x0325, 0x0353, 0x0382,
0x03b3, 0x03e5, 0x0418, 0x044d, 0x0484, 0x04bc, 0x04f6, 0x0532,
0x056f, 0x05ad, 0x05ed, 0x062f, 0x0673, 0x06b8, 0x06fe, 0x0747,
0x0791, 0x07dd, 0x082a, 0x087a, 0x08ca, 0x091d, 0x0972, 0x09c8,
0x0a20, 0x0a79, 0x0ad5, 0x0b32, 0x0b91, 0x0bf2, 0x0c55, 0x0cba,
0x0d20, 0x0d88, 0x0df2, 0x0e5e, 0x0ecc, 0x0f3c, 0x0fae, 0x1021,
0x1097, 0x110e, 0x1188, 0x1203, 0x1280, 0x1300, 0x1381, 0x1404,
0x1489, 0x1510, 0x159a, 0x1625, 0x16b2, 0x1741, 0x17d3, 0x1866,
0x18fb, 0x1993, 0x1a2c, 0x1ac8, 0x1b66, 0x1c06, 0x1ca7, 0x1d4c,
0x1df2, 0x1e9a, 0x1f44, 0x1ff1, 0x20a0, 0x2150, 0x2204, 0x22b9,
0x2370, 0x242a, 0x24e5, 0x25a3, 0x2664, 0x2726, 0x27eb, 0x28b1,
0x297b, 0x2a46, 0x2b14, 0x2be3, 0x2cb6, 0x2d8a, 0x2e61, 0x2f3a,
0x3015, 0x30f2, 0x31d2, 0x32b4, 0x3399, 0x3480, 0x3569, 0x3655,
0x3742, 0x3833, 0x3925, 0x3a1a, 0x3b12, 0x3c0b, 0x3d07, 0x3e06,
0x3f07, 0x400a, 0x4110, 0x4218, 0x4323, 0x4430, 0x453f, 0x4651,
0x4765, 0x487c, 0x4995, 0x4ab1, 0x4bcf, 0x4cf0, 0x4e13, 0x4f39,
0x5061, 0x518c, 0x52b9, 0x53e9, 0x551b, 0x5650, 0x5787, 0x58c1,
0x59fe, 0x5b3d, 0x5c7e, 0x5dc2, 0x5f09, 0x6052, 0x619e, 0x62ed,
0x643e, 0x6591, 0x66e8, 0x6840, 0x699c, 0x6afa, 0x6c5b, 0x6dbe,
0x6f24, 0x708d, 0x71f8, 0x7366, 0x74d7, 0x764a, 0x77c0, 0x7939,
0x7ab4, 0x7c32, 0x7db3, 0x7f37, 0x80bd, 0x8246, 0x83d1, 0x855f,
0x86f0, 0x8884, 0x8a1b, 0x8bb4, 0x8d50, 0x8eef, 0x9090, 0x9235,
0x93dc, 0x9586, 0x9732, 0x98e2, 0x9a94, 0x9c49, 0x9e01, 0x9fbb,
0xa179, 0xa339, 0xa4fc, 0xa6c2, 0xa88b, 0xaa56, 0xac25, 0xadf6,
0xafca, 0xb1a1, 0xb37b, 0xb557, 0xb737, 0xb919, 0xbaff, 0xbce7,
0xbed2, 0xc0c0, 0xc2b1, 0xc4a5, 0xc69c, 0xc895, 0xca92, 0xcc91,
0xce94, 0xd099, 0xd2a1, 0xd4ad, 0xd6bb, 0xd8cc, 0xdae0, 0xdcf7,
0xdf11, 0xe12e, 0xe34e, 0xe571, 0xe797, 0xe9c0, 0xebec, 0xee1b,
0xf04d, 0xf282, 0xf4ba, 0xf6f5, 0xf933, 0xfb74, 0xfdb8, 0xffff,
};
int32_t srgb_u8_to_linear_int(uint8_t x)
{
return (int32_t)srgb2linear[x];
}
You may have noticed that we are returning the value in a i32: this is to
ease arithmetic operations (preserving the 16-bit unsigned precision would have
overflow warping implications when working with the value).
Linear to OkLab
The OkLab is expressed in a virtually continuous space (floats). If we feed all 16.7 millions sRGB colors to the OkLab transform we get the following ranges in output:
min Lab: 0.000000 -0.233887 -0.311528
max Lab: 1.000000 0.276216 0.198570
We observe that L is always positive and neatly within [0,1] while a and
b are in a more restricted and signed range. Multiple choices are offered to
us with regard to the integer representation we pick.
Since we chose 16-bit for the input linear value, it makes sense to preserve
that precision for Lab. For the L component, this fits neatly ([0,1] in the ref
maps to [0,0xffff] in the integer version), but for the a and b
component, not so much. We could pick a signed 16-bit, but that would imply a
15-bit precision for the arithmetic and 1-bit for the sign, which is going to
be troublesome: we want to preserve the same precision for L, a and b
since the whole point of this operation is to have a uniform space.
Instead, I decided to go with 16-bits of precision, with one extra bit for the
sign (which will be used for a and b), and thus storing Lab in 3 signed
i32. Alternatively, we could decide to have a 15-bit precision with an extra
bit for the sign by using 3 i16. This should work mostly fine but having the
values fit exactly the boundaries of the storage can be problematic in various
situations, typically anything that involves boundary checks and overflows.
Picking a larger storage simplifies a bunch of things.
Looking at srgb_u8_to_oklab_f32 we quickly see that for most of the function
it's simple arithmetic, but we have a cube root (cbrt()), so let's study that first.
Cube root
All the cbrt inputs are driven by this:
const float l = 0.4122214708f * r + 0.5363325363f * g + 0.0514459929f * b;
const float m = 0.2119034982f * r + 0.6806995451f * g + 0.1073969566f * b;
const float s = 0.0883024619f * r + 0.2817188376f * g + 0.6299787005f * b;
This might not be obvious at first glance but here l, m and s all are in
[0,1] range (the sum of the coefficients of each row is 1), so we will only
need to deal with this range in our cbrt implementation. This simplifies
greatly the problem!
Now, what does it look like?
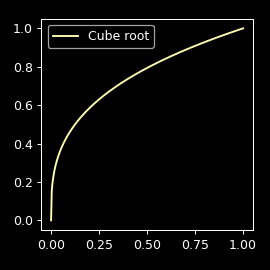
This function is simply the inverse of f(x)=x³, which is a more convenient
function to work with. And I have some great news: not long ago, I wrote an
article on how to inverse a function, so that's exactly what we
are going to do here: inverse f(x)=x³.
What we first need though is a good approximation of the curve. A straight line is probably fine but we could try to use some symbolic regression in order to get some sort of rough polynomial approximation. PySR can do that in a few lines of code:
import numpy as np
from pysr import PySRRegressor
# 25 points of ³√x within [0,1]
x = np.linspace(0, 1, 25).reshape(-1, 1)
y = x ** (1/3)
model = PySRRegressor(model_selection="accuracy", binary_operators=["+", "-", "*"], niterations=200)
r = model.fit(x, y, variable_names=["x"])
print(r)
The output is not deterministic for some reason (which is quite annoying) and
the expressions provided usually follows a wonky form. Still, in my run it
seemed to take a liking to the following polynomial: u₀ = x³ - 2.19893x² + 2.01593x + 0.219407 (reformatted in a sane polynomial form thanks to
WolframAlpha).
Warning
Increasing the number of data points is not really a good idea because we quickly start being confronted to Runge's phenomenon. No need to overthink it, 25 points is just fine.
Now we can make a few Newton iterations. For that, we need the derivative of f(u_n)=u_n^3-x, so f'(u_n)=3u_n^2 and thus the iteration expressions can be obtained easily:
If you don't understand what the hell is going on here, check the article referred to earlier, we're simply following the recipe here.
Now I had a look into how most libc compute cbrt, and despite
sometimes referring to Newton iterations, they were actually using Halley
iterations. So we're going to do the same (not lying, just
the Halley part). To get the Halley iteration instead of Newton, we need the
first but also the second derivative of f(u_n)=u_n^3-x (f'(u_n)=3u_n^2 and
f"(u_n)=6u_n) from which we deduce a relatively simple expression:
We have everything we need to approximate a cube root of a real between 0 and
1. In Python a complete implementation would be as simple as this snippet:
b, c, d = -2.19893, 2.01593, 0.219407
def cbrt01(x):
# We only support [0,1]
if x <= 0: return 0
if x >= 1: return 1
# Initial approximation
u = x**3 + b*x**2 + c*x + d
# 2 Halley iterations
u = u * (2*x+u**3) / (x+2*u**3)
u = u * (2*x+u**3) / (x+2*u**3)
return u
But now we need to scale the floating values up into 16-bit integers.
First of all, in the integer version our x is actually in K scale, which means we want to express u according to X=xK. Similarly, we want to use B=bK, C=cK and D=dK instead of b, c and d because we have no way of expressing the former as integer otherwise. Finally, we're not actually going to compute u_0 but u_{0}K because we're preserving the scale through the function. We have:
With this we have a relatively cheap expression where the K divisions would still preserve enough precision even if evaluated as integer division.
We can do the same for the Halley iteration. I spare you the algebra, the expression u(2x+u^3) / (x+2u^3) becomes (U(2X+U^3/K^2)) / (X+2U^3/K^2).
Looking at this expression you may start to worry about overflows, and that
would fair since even K^2 is getting dangerously close to the sun (it's
actually already larger than INT32_MAX). For this reason we're going to cheat
and simply use 64-bit arithmetic in this function. I believe we could reduce
the risk of overflow, but I don't think there is a way to remain in 32-bit
without nasty compromises anyway. This is also why in the code below you'll
notice the constants are suffixed with LL (to force long-long/64-bit
arithmetic).
Warning
Beware that overflows are a terrible predicament to get into as they will
lead to an undefined behavior. Do not underestimate this risk. You
might not detect them early enough, and missing them may mislead you when
interpreting the results. For this reason, I strongly suggest to always
build with -fsanitize=undefined during test and development. I don't
do that often, but for this kind of research, I also highly recommend
to first write tests that cover all possible integers input (when
applicable) so that overflows are detected as soon as possible.
Before we write the integer version of our function, we need to address
rounding. In the case of the initial approximation I don't think we need to
bother, but for our Halley iteration we're going to need as much precision as
we can get. Since we know U is positive (remember we're evaluating cbrt(x)
where x is in [0,1]), we can use the (a+b/2)/b rounding
formula.
Our function finally just looks like:
#define K2 ((int64_t)K*K)
int32_t cbrt01_int(int32_t x)
{
int64_t u;
/* Approximation curve is for the [0,1] range */
if (x <= 0) return 0;
if (x >= K) return K;
/* Initial approximation: x³ - 2.19893x² + 2.01593x + 0.219407 */
u = x*(x*(x - 144107LL) / K + 132114LL) / K + 14379LL;
/* Refine with 2 Halley iterations. */
for (int i = 0; i < 2; i++) {
const int64_t u3 = u*u*u;
const int64_t den = x + (2*u3 + K2/2) / K2;
u = (u * (2*x + (u3 + K2/2) / K2) + den/2) / den;
}
return u;
}
Cute, isn't it? If we test the accuracy of this function by calling it for all the possible values we actually get extremely good results. Here is a test code:
int main(void)
{
float max_diff = 0;
float total_diff = 0;
for (int i = 0; i <= K; i++) {
const float ref = cbrtf(i / (float)K);
const float out = cbrt01_int(i) / (float)K;
const float d = fabs(ref - out);
if (d > max_diff)
max_diff = d;
total_diff += d;
}
printf("max_diff=%f total_diff=%f avg_diff=%f\n",
max_diff, total_diff, total_diff / (K + 1));
return 0;
}
Output: max_diff=0.030831 total_diff=0.816078 avg_diff=0.000012
If we want to trade precision for speed, we could adjust the function to use Newton iterations, and maybe remove the rounding.
Back to the core
Going back to our sRGB-to-OkLab function, everything should look
straightforward to implement now. There is one thing though, while lms
computation (at the beginning of the function) is exclusively working with
positive values, the output Lab value expression is signed. For this reason
we will need a more involved rounded division, so referring again to my last
article we will use:
static int64_t div_round64(int64_t a, int64_t b) { return (a^b)<0 ? (a-b/2)/b : (a+b/2)/b; }
And thus, we have:
struct LabInt { int32_t L, a, b; };
struct LabInt srgb_u8_to_oklab_int(uint32_t srgb)
{
const int32_t r = (int32_t)srgb2linear[srgb >> 16 & 0xff];
const int32_t g = (int32_t)srgb2linear[srgb >> 8 & 0xff];
const int32_t b = (int32_t)srgb2linear[srgb & 0xff];
// Note: lms can actually be slightly over K due to rounded coefficients
const int32_t l = (27015LL*r + 35149LL*g + 3372LL*b + K/2) / K;
const int32_t m = (13887LL*r + 44610LL*g + 7038LL*b + K/2) / K;
const int32_t s = (5787LL*r + 18462LL*g + 41286LL*b + K/2) / K;
const int32_t l_ = cbrt01_int(l);
const int32_t m_ = cbrt01_int(m);
const int32_t s_ = cbrt01_int(s);
const struct LabInt ret = {
.L = div_round64( 13792LL*l_ + 52010LL*m_ - 267LL*s_, K),
.a = div_round64(129628LL*l_ - 159158LL*m_ + 29530LL*s_, K),
.b = div_round64( 1698LL*l_ + 51299LL*m_ - 52997LL*s_, K),
};
return ret;
}
The note in this code is here to remind us that we have to saturate lms to a
maximum of K (corresponding to 1.0 with floats), which is what we're doing
in cbrt01_int().
At this point we can already work within the OkLab space but we're only half-way through the pain. Fortunately, things are going to be easier from now on.
OkLab to sRGB
Our OkLab-to-sRGB function relies on the Linear-to-sRGB function (at the end), so we're going to deal with it first.
Linear to sRGB
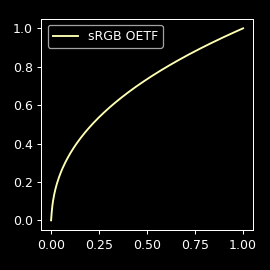
Contrary to sRGB-to-Linear it's going to be tricky to rely on a table because
it would be way too large to hold all possible values (since it would require
K entries). I initially considered computing powf(x, 1.f/2.4f) with integer
arithmetic somehow, but this is much more involved than how we managed to
implement cbrt. So instead I thought about approximating the curve with a
bunch of points (stored in a table), and then approximate any intermediate
value with a linear interpolation, that is as if the point were joined through
small segments.
We gave 256 16-bit entries to srgb2linear, so if we were to give as much
storage to linear2srgb we could have a table of 512 8-bit entries (our output
is 8-bit). Here it is:
/**
* Table mapping formula:
* f(x) = x < 0.0031308 ? x*12.92 : (1.055)*x^(1/2.4)-0.055 (sRGB OETF)
* Where x is the normalized index in the table and f(x) the value in the table.
* f(x) is remapped to [0,0xff] and rounded.
*
* Since a 16-bit table is too large, we reduce its precision to 9-bit.
*/
static const uint8_t linear2srgb[P + 1] = {
0x00, 0x06, 0x0d, 0x12, 0x16, 0x19, 0x1c, 0x1f, 0x22, 0x24, 0x26, 0x28, 0x2a, 0x2c, 0x2e, 0x30,
0x32, 0x33, 0x35, 0x36, 0x38, 0x39, 0x3b, 0x3c, 0x3d, 0x3e, 0x40, 0x41, 0x42, 0x43, 0x45, 0x46,
0x47, 0x48, 0x49, 0x4a, 0x4b, 0x4c, 0x4d, 0x4e, 0x4f, 0x50, 0x51, 0x52, 0x53, 0x54, 0x55, 0x56,
0x56, 0x57, 0x58, 0x59, 0x5a, 0x5b, 0x5b, 0x5c, 0x5d, 0x5e, 0x5f, 0x5f, 0x60, 0x61, 0x62, 0x62,
0x63, 0x64, 0x65, 0x65, 0x66, 0x67, 0x67, 0x68, 0x69, 0x6a, 0x6a, 0x6b, 0x6c, 0x6c, 0x6d, 0x6e,
0x6e, 0x6f, 0x6f, 0x70, 0x71, 0x71, 0x72, 0x73, 0x73, 0x74, 0x74, 0x75, 0x76, 0x76, 0x77, 0x77,
0x78, 0x79, 0x79, 0x7a, 0x7a, 0x7b, 0x7b, 0x7c, 0x7d, 0x7d, 0x7e, 0x7e, 0x7f, 0x7f, 0x80, 0x80,
0x81, 0x81, 0x82, 0x82, 0x83, 0x84, 0x84, 0x85, 0x85, 0x86, 0x86, 0x87, 0x87, 0x88, 0x88, 0x89,
0x89, 0x8a, 0x8a, 0x8b, 0x8b, 0x8c, 0x8c, 0x8c, 0x8d, 0x8d, 0x8e, 0x8e, 0x8f, 0x8f, 0x90, 0x90,
0x91, 0x91, 0x92, 0x92, 0x93, 0x93, 0x93, 0x94, 0x94, 0x95, 0x95, 0x96, 0x96, 0x97, 0x97, 0x97,
0x98, 0x98, 0x99, 0x99, 0x9a, 0x9a, 0x9a, 0x9b, 0x9b, 0x9c, 0x9c, 0x9c, 0x9d, 0x9d, 0x9e, 0x9e,
0x9f, 0x9f, 0x9f, 0xa0, 0xa0, 0xa1, 0xa1, 0xa1, 0xa2, 0xa2, 0xa3, 0xa3, 0xa3, 0xa4, 0xa4, 0xa5,
0xa5, 0xa5, 0xa6, 0xa6, 0xa6, 0xa7, 0xa7, 0xa8, 0xa8, 0xa8, 0xa9, 0xa9, 0xa9, 0xaa, 0xaa, 0xab,
0xab, 0xab, 0xac, 0xac, 0xac, 0xad, 0xad, 0xae, 0xae, 0xae, 0xaf, 0xaf, 0xaf, 0xb0, 0xb0, 0xb0,
0xb1, 0xb1, 0xb1, 0xb2, 0xb2, 0xb3, 0xb3, 0xb3, 0xb4, 0xb4, 0xb4, 0xb5, 0xb5, 0xb5, 0xb6, 0xb6,
0xb6, 0xb7, 0xb7, 0xb7, 0xb8, 0xb8, 0xb8, 0xb9, 0xb9, 0xb9, 0xba, 0xba, 0xba, 0xbb, 0xbb, 0xbb,
0xbc, 0xbc, 0xbc, 0xbd, 0xbd, 0xbd, 0xbe, 0xbe, 0xbe, 0xbf, 0xbf, 0xbf, 0xc0, 0xc0, 0xc0, 0xc1,
0xc1, 0xc1, 0xc1, 0xc2, 0xc2, 0xc2, 0xc3, 0xc3, 0xc3, 0xc4, 0xc4, 0xc4, 0xc5, 0xc5, 0xc5, 0xc6,
0xc6, 0xc6, 0xc6, 0xc7, 0xc7, 0xc7, 0xc8, 0xc8, 0xc8, 0xc9, 0xc9, 0xc9, 0xc9, 0xca, 0xca, 0xca,
0xcb, 0xcb, 0xcb, 0xcc, 0xcc, 0xcc, 0xcc, 0xcd, 0xcd, 0xcd, 0xce, 0xce, 0xce, 0xce, 0xcf, 0xcf,
0xcf, 0xd0, 0xd0, 0xd0, 0xd0, 0xd1, 0xd1, 0xd1, 0xd2, 0xd2, 0xd2, 0xd2, 0xd3, 0xd3, 0xd3, 0xd4,
0xd4, 0xd4, 0xd4, 0xd5, 0xd5, 0xd5, 0xd6, 0xd6, 0xd6, 0xd6, 0xd7, 0xd7, 0xd7, 0xd7, 0xd8, 0xd8,
0xd8, 0xd9, 0xd9, 0xd9, 0xd9, 0xda, 0xda, 0xda, 0xda, 0xdb, 0xdb, 0xdb, 0xdc, 0xdc, 0xdc, 0xdc,
0xdd, 0xdd, 0xdd, 0xdd, 0xde, 0xde, 0xde, 0xde, 0xdf, 0xdf, 0xdf, 0xe0, 0xe0, 0xe0, 0xe0, 0xe1,
0xe1, 0xe1, 0xe1, 0xe2, 0xe2, 0xe2, 0xe2, 0xe3, 0xe3, 0xe3, 0xe3, 0xe4, 0xe4, 0xe4, 0xe4, 0xe5,
0xe5, 0xe5, 0xe5, 0xe6, 0xe6, 0xe6, 0xe6, 0xe7, 0xe7, 0xe7, 0xe7, 0xe8, 0xe8, 0xe8, 0xe8, 0xe9,
0xe9, 0xe9, 0xe9, 0xea, 0xea, 0xea, 0xea, 0xeb, 0xeb, 0xeb, 0xeb, 0xec, 0xec, 0xec, 0xec, 0xed,
0xed, 0xed, 0xed, 0xee, 0xee, 0xee, 0xee, 0xef, 0xef, 0xef, 0xef, 0xef, 0xf0, 0xf0, 0xf0, 0xf0,
0xf1, 0xf1, 0xf1, 0xf1, 0xf2, 0xf2, 0xf2, 0xf2, 0xf3, 0xf3, 0xf3, 0xf3, 0xf3, 0xf4, 0xf4, 0xf4,
0xf4, 0xf5, 0xf5, 0xf5, 0xf5, 0xf6, 0xf6, 0xf6, 0xf6, 0xf6, 0xf7, 0xf7, 0xf7, 0xf7, 0xf8, 0xf8,
0xf8, 0xf8, 0xf9, 0xf9, 0xf9, 0xf9, 0xf9, 0xfa, 0xfa, 0xfa, 0xfa, 0xfb, 0xfb, 0xfb, 0xfb, 0xfb,
0xfc, 0xfc, 0xfc, 0xfc, 0xfd, 0xfd, 0xfd, 0xfd, 0xfd, 0xfe, 0xfe, 0xfe, 0xfe, 0xff, 0xff, 0xff,
};
Again we're going to start with the floating point version as it's easier to reason with.
We have a precision P of 9-bits: P = (1<<9)-1 = 511 = 0x1ff. But for the
sake of understanding the math, the following diagram will assume a P of 3
so that we can clearly see the segment divisions:
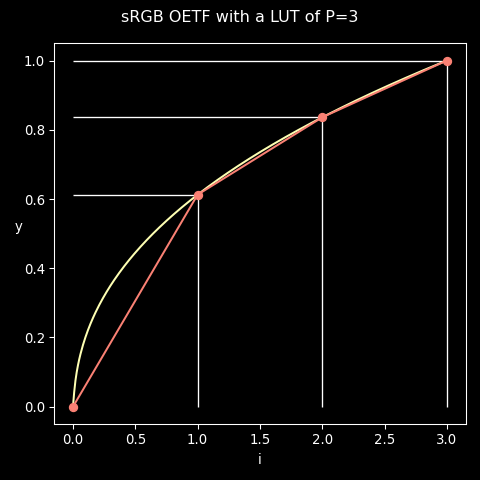
The input of our table is an integer index which needs to be calculated
according to our input x. But as stated earlier, we won't need one but two
indices in order to interpolate a point between 2 discrete values from our
table. We will refer to these indices as iₚ and iₙ, which can be computed
like this:
(\lfloor a \rfloor means floor(a))
In order to get an approximation of y according to i, we simply need a linear remapping: the ratio of i between i_p and i_n is the same ratio as y between y_p and y_n. So yet again we're going to rely on the most useful maths formulas: \mathrm{remap}(i_p,i_n,y_p,y_n,i) = \mathrm{mix}(y_p,y_n,\mathrm{linear}(i_p,i_n,i)).
The ratio r we're computing as an input to the y-mix can be simplified a bit:
So in the end our formula is simply: y = mix(y_p,y_n,\mathrm{fract}(xP))
Translated into C we can write it like this:
uint8_t linear_f32_to_srgb_u8_fast(float x)
{
if (x <= 0.f) {
return 0;
} else if (x >= 1.f) {
return 0xff;
} else {
const float i = x * P;
const int32_t idx = (int32_t)floorf(i);
const float y0 = linear2srgb[idx];
const float y1 = linear2srgb[idx + 1];
const float r = i - idx;
return lrintf(mix(y0, y1, r));
}
}
Note
In case you are concerned about idx+1 overflowing,
floorf((1.0-FLT_EPSILON)*P) is P-1, so this is safe.
Linear to sRGB, integer version
In the integer version, our function input x is within [0,K], so we need to
make a few adjustments.
The first issue we have is that with integer arithmetic our i and idx are
the same. We have X=x·K as input, so i = idx = X·P/K because we are using
an integer division, which in this case is equivalent to the floor()
expression in the float version. So while it's a simple and fast way to get
yₚ and yₙ, we have an issue figuring out the ratio r.
One tool we have is the modulo operator: the integer division is destructive of the fractional part, but fortunately the modulo (the rest of the division) gives this information back. It can also be obtained for free most of the time because CPU division instructions tend to also provide that modulo as well without extra computation.
If we give m = (X·P) % K, we have the fractional part of the division
expressed in the K scale, which means we can derivate our ratio r from it:
r = m / K.
Slipping the K division in our mix() expression we end up with the
following code:
uint8_t linear_int_to_srgb_u8(int32_t x)
{
if (x <= 0) {
return 0;
} else if (x >= K) {
return 0xff;
} else {
const int32_t xP = x * P;
const int32_t i = xP / K;
const int32_t m = xP % K;
const int32_t y0 = linear2srgb[i];
const int32_t y1 = linear2srgb[i + 1];
return (m * (y1 - y0) + K/2) / K + y0;
}
}
Testing this function for all the possible input of x, the biggest inaccuracy
is an off-by-one, which concerns 6280 of the 65536 possible values (less than
10%): 2886 "off by -1" and 3394 "off by +1". It matches exactly the inaccuracy
of the float version of this function, so I think we can be pretty happy with it.
Given how good this approach is, we could also consider applying the same
strategy for cbrt, so this is left as an exercise to the reader.
Back to the core
We're finally in our last function. Using everything we've learned so far, it can be trivially converted to integer arithmetic:
uint32_t oklab_int_to_srgb_u8(struct LabInt c)
{
const int64_t l_ = c.L + div_round64(25974LL * c.a, K) + div_round64( 14143LL * c.b, K);
const int64_t m_ = c.L + div_round64(-6918LL * c.a, K) + div_round64( -4185LL * c.b, K);
const int64_t s_ = c.L + div_round64(-5864LL * c.a, K) + div_round64(-84638LL * c.b, K);
const int32_t l = l_*l_*l_ / K2;
const int32_t m = m_*m_*m_ / K2;
const int32_t s = s_*s_*s_ / K2;
const uint8_t r = linear_int_to_srgb_u8((267169LL * l - 216771LL * m + 15137LL * s + K/2) / K);
const uint8_t g = linear_int_to_srgb_u8((-83127LL * l + 171030LL * m - 22368LL * s + K/2) / K);
const uint8_t b = linear_int_to_srgb_u8(( -275LL * l - 46099LL * m + 111909LL * s + K/2) / K);
return r<<16 | g<<8 | b;
}
Important things to notice:
- We're storing
l_,m_ands_in 64-bits values so that the following cubic do not overflow - We're using
div_round64for part of the expressions ofl_,m_ands_because they are using signed sub-expressions - We're using a naive integer division in
r,gandbbecause the value is expected to be positive
Evaluation
We're finally there. In the end the complete code is less than 200 lines of
code and even less for the optimized float one (assuming we don't implement our
own cbrt). The complete code, test functions and benchmarks tools can be
found on GitHub.
Accuracy
Comparing the integer version to the reference float gives use the following results:
- sRGB to OkLab:
max_diff=0.000883 total_diff=0.051189 - OkLab to sRGB:
max_diff_r=2 max_diff_g=1 max_diff_b=1
I find these results pretty decent for an integer version, but you're free to disagree and improve them.
Speed
The benchmarks are also interesting: on my main workstation (Intel® Core™ i7-12700, glibc 2.36, GCC 12.2.0), the integer arithmetic is slightly slower that the optimized float version:
| Command | Mean [s] | Min [s] | Max [s] | Relative |
|---|---|---|---|---|
| Reference | 1.425 ± 0.008 | 1.414 | 1.439 | 1.59 ± 0.01 |
| Fast float | 0.897 ± 0.005 | 0.888 | 0.902 | 1.00 |
| Integer arithmetic | 0.937 ± 0.006 | 0.926 | 0.947 | 1.04 ± 0.01 |
Observations:
- The FPU is definitely fast in modern CPUs
- Both integer and optimized float versions are destroying the reference code (note that this only because of the transfer functions optimizations, as we have no change in the OkLab functions themselves in the optimized float version)
On the other hand, on one of my random ARM board (NanoPI NEO 2 with a Cortex A53, glibc 2.35, GCC 12.1.0), I get different results:
| Command | Mean [s] | Min [s] | Max [s] | Relative |
|---|---|---|---|---|
| Reference | 27.678 ± 0.009 | 27.673 | 27.703 | 2.04 ± 0.00 |
| Fast float | 15.769 ± 0.001 | 15.767 | 15.772 | 1.16 ± 0.00 |
| Integer arithmetic | 13.551 ± 0.001 | 13.550 | 13.553 | 1.00 |
Not that much faster proportionally speaking, but the integer version is still significantly faster overall on such low-end device.
Conclusion
This took me ages to complete, way longer than I expected but I'm pretty happy with the end results and with everything I learned in the process. Also, you may have noticed how much I referred to previous work; this has been particularly satisfying from my point of view (re-using previous toolboxes means they were actually useful). This write-up won't be an exception to the rule: in a later article, I will make use of OkLab for another project I've been working on for a while now. See you soon!