A while ago, I had some fun writing a solution for the classic eight queens puzzle. But rather than focusing on the recursive issue which is finally just a dozen of SLOC, I played with the board representation in memory. The recursive algorithm won't be much detailed here, it's not the aim of this post.
Plate declaration
We need a 8x8 array to represent the plate, so instinctively, we start with the following declaration:
int t[8][8];
Then, we realized a two-dimensional array is not specially useful since we'll brute-force with an index from 0 to 63:
int t[64];
An int is a bit overkill for a boolean value, isn't it?
uint8_t t[64];
Hey, maybe could just use 8 bits per line:
uint8_t t[8];
Right, so we have 8x8 bits, then let's use a simpler representation:
uint64_t t;
Here we go, much better. We can now start.
ASCII art
Being able to visually represent our board is the first thing to do. Here is an example:
static void disp_board(uint64_t t)
{
uint64_t mask = 1;
for (int i = 0; i < 64; i++, mask <<= 1)
printf("%c%c", t & mask ? '@' : '.', (i + 1) % 8 == 0 ? '\n' : ' ');
printf("\n");
}
This function displays:
@ . . . . . . .
. . . . @ . . .
. . . . . . . @
. . . . . @ . .
. . @ . . . . .
. . . . . . @ .
. @ . . . . . .
. . . @ . . . .
...for t = 577094088726155265, or in binary:
00001000 00000010 01000000 00000100 00100000 10000000 00010000 00000001
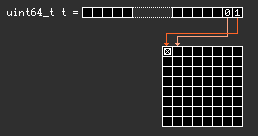
You'll notice I choose the LSb for the bit corresponding to the position
(0, 0) on the board (1 means a queen, 0 means no queen).
Recursion
About the recursion, here is the code with the appropriate main():
#define sq(i) do { t |= 1ULL << i; qleft--; } while (0)
#define rq(i) do { t &= ~(1ULL << i); qleft++; } while (0)
static int solve(uint64_t t, int qleft, int idx)
{
int n = 0;
if (idx == 64)
return 0;
if (ok(t, idx)) {
sq(idx);
if (qleft == 0) {
disp_board(t);
n = 1;
} else {
n = solve(t, qleft, (idx / 8 + 1) * 8);
}
rq(idx);
}
return n + solve(t, qleft, idx + 1);
}
int main()
{
printf("%d\n", solve(0, 8, 0));
return 0;
}
A few notes on this code:
- The macros
sqandrq(respectivelyset queenandremove queen) set and unset the queen's bit with indexidx, and increment/decrement the number of left queens to place. - The
ok()function we will study soon let you know if it's possible to put a queen at indexidxor not. - The
main()function runs the recursion with an empty board (t=0), eight queens left to place (qleft=8) starting at positionidx=0, or(0,0). - When all the queens are set, we display the plate, and we continue.
solve()returns the number of solutions when we found and displayed them all.
Masquerade ball, part I
The fun can now begin with the writing of the last function:
static int ok(uint64_t t, int idx);
To simplify a few operations, we fetch the x and y coordinates:
static int ok(uint64_t t, int idx)
{
int y = idx / 8;
int x = idx - y * 8;
// ...
}
And the function's return will look like something like this:
return !(t & (MASK_LINE | MASK_COLUMN | MASK_DIAGONAL1 | MASK_DIAGONAL2));
All the masks will form a bit field in which no queen should be. A simple
binary AND with the board will allow to say if it's the case or not.
Let's start by determining MASK_LINE for a given idx. A mask for the line
could be the following:
#define MLI 0x00000000000000ffULL /* 00000000 00000000 00000000 00000000 00000000 00000000 00000000 11111111 */
This mask allow to scratch the first line of the board, so we need to shift it to the given queen line:
#define MASK_LINE(y) (MLI << (y) * 8)

And in the same way for the columns starting with the left one:
#define MCL 0x0101010101010101ULL /* 00000001 00000001 00000001 00000001 00000001 00000001 00000001 00000001 */
#define MASK_COLUMN(x) (MCL << (x))
Masquerade ball, part II
Since we have the two masks for lines and columns, we now need to do the diagonals. Let's take the first case:
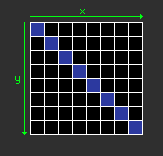
If we take the case where x > y, we have to shift to the left (the right on
the board) eight time the difference:

However, the diagonal gets extended (red frame) while it shouldn't, so we need
to filter that part. For this diagonal and x > y, we can use the following
mask:
d = x - y
(MD1 & ~0ULL >> 8 * d) << d
^ ^^^^^ ^^^^^ ^^^^
| | | |
| | | `-- 4. And we shift the diagonal.
| | |
| | `-- 2. ...we shift them in order to create zeroes in the lowest part of the board.
| |
| `-- 1. All bits to 1...
|
`-- 3. We only keep higher part of the board.
With MD1 (mask for the middle diagonal):
#define MD1 0x8040201008040201ULL /* 10000000 01000000 00100000 00010000 00001000 00000100 00000010 00000001 */
To handle the case where x < y, we just have to shift in the other direction,
and toggle the difference sign:
d = x - y
(d > 0 ? (MD1 & ~0ULL >> 8 * d) << d : (MD1 & ~0ULL << 8 * -d) >> -d)
^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
Shift to the right on the Shift to the left on the board.
board.
The case for the second diagonal is almost the same; the difference is not
obtained with x - y but x + y - 7, and the mask change:
d1 = x - y
d2 = x + y - 7
First diagonal: (d1 > 0 ? (MD1 & ~0ULL >> 8 * d1) << d1 : (MD1 & ~0ULL << 8 * -d1) >> -d1)
Second diagonal: (d2 > 0 ? (MD2 & ~0ULL << 8 * d2) << d2 : (MD2 & ~0ULL >> 8 * -d2) >> -d2)
With the following MD2:
#define MD2 0x0102040810204080ULL /* 00000001 00000010 00000100 00001000 00010000 00100000 01000000 10000000 */
If we now merge our four masks (line, column, diagonal 1 and diagonal 2), we get this code:
#define MLI 0x00000000000000ffULL /* 00000000 00000000 00000000 00000000 00000000 00000000 00000000 11111111 */
#define MCL 0x0101010101010101ULL /* 00000001 00000001 00000001 00000001 00000001 00000001 00000001 00000001 */
#define MD1 0x8040201008040201ULL /* 10000000 01000000 00100000 00010000 00001000 00000100 00000010 00000001 */
#define MD2 0x0102040810204080ULL /* 00000001 00000010 00000100 00001000 00010000 00100000 01000000 10000000 */
static int ok(uint64_t t, int idx)
{
int y = idx / 8;
int x = idx - y * 8;
int d1 = x - y;
int d2 = x + y - 7;
return !(t & ((MLI << y * 8) | (MCL << x)
| (d1 > 0 ? (MD1 & ~0ULL >> 8 * d1) << d1 : (MD1 & ~0ULL << 8 * -d1) >> -d1)
| (d2 > 0 ? (MD2 & ~0ULL << 8 * d2) << d2 : (MD2 & ~0ULL >> 8 * -d2) >> -d2)));
}
The result is a binary AND between the memory board, and a mask which looks
like for example:
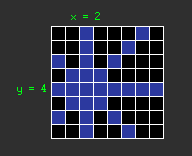
Conclusion
We can do better, with less than 64 bits, but I found this approach entertaining (and I got this last link when I was almost done with my code).
For those interested, here is the complete code:
#include <stdio.h>
#include <stdint.h>
static void disp_board(uint64_t t)
{
uint64_t mask = 1;
printf("t = %llx\n", t);
for (int i = 0; i < 64; i++, mask <<= 1)
printf("%c%c", t & mask ? '@' : '.', (i + 1) % 8 == 0 ? '\n' : ' ');
printf("\n");
}
#define MLI 0x00000000000000ffULL /* 00000000 00000000 00000000 00000000 00000000 00000000 00000000 11111111 */
#define MCL 0x0101010101010101ULL /* 00000001 00000001 00000001 00000001 00000001 00000001 00000001 00000001 */
#define MD1 0x8040201008040201ULL /* 10000000 01000000 00100000 00010000 00001000 00000100 00000010 00000001 */
#define MD2 0x0102040810204080ULL /* 00000001 00000010 00000100 00001000 00010000 00100000 01000000 10000000 */
static int ok(uint64_t t, int idx)
{
int y = idx / 8;
int x = idx - y * 8;
int d1 = x - y;
int d2 = x + y - 7;
return !(t & ((MLI << y * 8) | (MCL << x)
| (d1 > 0 ? (MD1 & ~0ULL >> 8 * d1) << d1 : (MD1 & ~0ULL << 8 * -d1) >> -d1)
| (d2 > 0 ? (MD2 & ~0ULL << 8 * d2) << d2 : (MD2 & ~0ULL >> 8 * -d2) >> -d2)));
}
#define sq(i) do { t |= 1ULL << i; qleft--; } while (0)
#define rq(i) do { t &= ~(1ULL << i); qleft++; } while (0)
static int solve(uint64_t t, int qleft, int idx)
{
int n = 0;
if (idx == 64)
return 0;
if (ok(t, idx)) {
sq(idx);
if (qleft == 0) {
disp_board(t);
n = 1;
} else {
n = solve(t, qleft, (idx / 8 + 1) * 8);
}
rq(idx);
}
return n + solve(t, qleft, idx + 1);
}
int main()
{
printf("%d\n", solve(0, 8, 0));
return 0;
}