Text rendering and effects using GPU-computed distances

Text rendering is cursed. Anyone who has worked on text will tell you the same; whether it's about layout, bi-directional, shaping, Unicode, or the rendering itself, it's never a completely solved problem. In my personal case, I've been working on trying to render text in the context of a compositing engine for creative content. I needed crazy text effects, and I needed them to be reasonably fast, which implied working with the GPU as much as possible. The distance field was an obvious requirement because it unlocks anti-aliasing and the ability to make many great effects for basically free.

In this article, we will see how to compute signed distance field on the GPU because it's much faster than doing it on the CPU, especially when targeting mobile devices. We will make the algorithm decently fast, then after lamenting about the limitations, we will see what kind of effects this opens up.

Extraction of glyph outlines

Non-bitmap fonts contain glyphs defined by outlines made of closed sequences of lines and (quadratic or cubic) Bézier curves. Extracting them isn't exactly complicated: FreeType or ttf-parser typically expose a way to do that.

For the purpose of this article, we're going to hard code the list of the Bézier curves inside the shader, but of course in a more serious setup those would be uploaded through storage buffers or similar.

Using this tiny program, a glyph can be dumped as series of outlines into a fixed size array:

struct Bezier {
    vec2 p0; // start point
    vec2 p1; // control point 1
    vec2 p2; // control point 2
    vec2 p3; // end point
};

#define N 42
#define NC 2
const int glyph_A_count[2] = int[](33, 9);
const Bezier glyph_A[42] = Bezier[](
    Bezier(vec2(  0.365370,  -0.570817), vec2(  0.374708,  -0.631518), vec2(  0.332685,  -0.687549), vec2(  0.339689,  -0.748249)),
    Bezier(vec2(  0.339689,  -0.748249), vec2(  0.339689,  -0.748249), vec2(  0.344358,  -0.764591), vec2(  0.351362,  -0.771595)),
    Bezier(vec2(  0.351362,  -0.771595), vec2(  0.384047,  -0.822957), vec2(  0.402724,  -0.855642), vec2(  0.442412,  -0.885992)),
    // ...
);

glyph_A_count contains how many Bézier curves there is for each sub-shape composing the glyph, and glyph_A contains that list of Bézier cubic curves.

Even though glyphs are also composed of lines and quadratic curves, we expand them all into cubics: "who can do more can do less".

We use these formulas to respectively expand lines and quadratics into cubics:

Where P_n are the Bézier control points.

For simplicity and because we want to make sure the most complex case is well tested, we will stick to this approach in this article. But it also means there is a lot of room for further optimizations. Since solving linear and quadratics is much simpler, this is left as an exercise for the reader.

Signed distance to the shape

In the previous article, we saw how to get the distance to a cubic Bézier curve. Each glyph being composed of multiple outlines, we can simply run over all of them and pick the shortest distance.

float get_distance(vec2 p, Bezier buf[N], int counts[NC]) {
    int base = 0;
    float dist = 1e38;

    for (int j = 0; j < NC; j++) {
        int count = counts[j];

        for (int i = 0; i < count; i++) {
            Bezier b = buf[base + i];
            float d = bezier_sq(p, b.p0, b.p1, b.p2, b.p3);
            dist = min(dist, d);
        }

        base += count;
    }

    return sqrt(dist);
}

Where bezier_sq() is the distance to the Bézier curve, squared, as defined in the previous article.

This works just fine, but as you can imagine, it's not cheap to solve so many distances per pixel. A first straightforward optimization would be to ignore any curve with a bounding box further than our currently best distance, because none of them can give a shorter one:

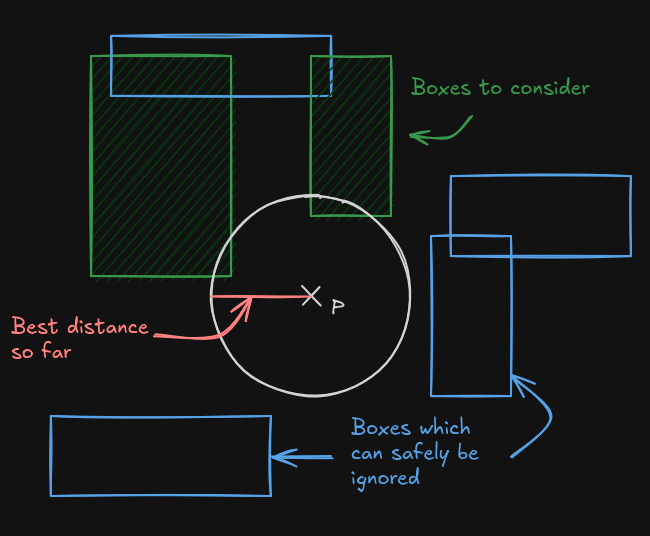
Where each box encloses a Bézier curve like this:

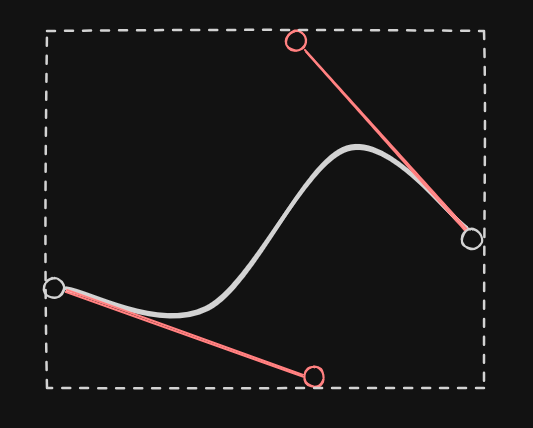
We could use a tighter bound but it would require more computation so this felt like a good trade-off.

Implementing this in the inner loop is pretty simple:

for (int i = 0; i < count; i++) {
    Bezier b = buf[base + i];
    vec2 p0=b.p0, p1=b.p1, p2=b.p2, p3=b.p3;

    // Distance to box (0 if inside), squared
    vec2 q0 = min(p0, min(p1, min(p2, p3)));
    vec2 q1 = max(p0, max(p1, max(p2, p3)));
    vec2 v = max(abs(q0+q1-p-p)-q1+q0, 0.)*.5;
    float h = dot(v,v);

    // We can't get a shorter distance than h if we were to compute the
    // distance to that curve
    if (h > dist)
        continue;

    float d = bezier_sq(p, p0, p1, p2, p3);
    dist = min(dist, d);
}

The distance to the bounding box formula comes from this explicative video by Inigo Quilez (the basic one, without the inside distance), adapted to the Bézier control point coordinates.

This saves a lot of computation in certain cases, but the worst case is still pretty terrible, as shown by the heat map of this 'C' glyph:

Indeed sometimes, it takes a long time to reach a good Bézier curve that is small enough to disregard most of the others. We observe it the further we go away from the beginning of the shape.

So the next step is to find a good initial candidate. One cheap way to do that is to first compute the distance to the center point of each curve, and pick the smallest:

// Find a good initial guess
int best = 0;
float boxd = 1e38;
for (int i = 0; i < count; i++) {
    Bezier b = buf[base + i];
    vec2 p0=b.p0, p1=b.p1, p2=b.p2, p3=b.p3;
    vec2 q0 = min(p0, min(p1, min(p2, p3)));
    vec2 q1 = max(p0, max(p1, max(p2, p3)));
    vec2 v = (q0+q1)*.5 - p;
    float h = dot(v,v);
    if (h < boxd)
        best=i, boxd=h;
}

// Initial guess
Bezier bb = buf[base + best];
dist = min(dist, bezier_sq(p, bb.p0, bb.p1, bb.p2, bb.p3));

for (int i = 0; i < count; i++) {
    if (i == best) // We already computed this one
        continue;

    Bezier b = buf[base + i];
    vec2 p0=b.p0, p1=b.p1, p2=b.p2, p3=b.p3;
    // ...

This optimization is immediately reflected on the heat map, where only the central point seems to become a critical point (this glyph is a pathological case as it forms a circle):

Winding number

The last step is to figure out whether we are inside or outside the shape. There are two schools here, the even-odd and the non-zero rules. We'll pick the latter because that's the expectation in the case of font rendering.

In deconstructing Bézier curves, we explained the theory of that specific algorithm so we're not going to dive into the details again. The basic idea is to strike a ray in one direction from our current position, and get how many times we cross a given curve. Here we will arbitrarily choose a horizontal ray line y = P_y where P is our current coordinate.

The topology of each curve can hint us on whether it's worth considering it or not. For example, if every control point is above or below our current position, it can be ignored. We can store all the signs in a mask and bail out as soon as the ray is either completely below or completely above the bounding box of the curve:

int signs = int(p0.y < p.y)
          | int(p1.y < p.y) << 1
          | int(p2.y < p.y) << 2
          | int(p3.y < p.y) << 3;
if (signs == 0 || signs == 15) // all signs are identical
    return 0;

Each sign indicates the position of the control point with regard to the ray. We can use the relative position of the starting point as a reference for the overall orientation (if there is a crossing, we know it will come from below or above):

int inc = (signs & 1) == 0 ? 1 : -1;

We also need to convert the Bézier curves to the usual polynomial at^3+bt^2+ct+d:

vec2 a = -p0 + 3.*(p1 - p2) + p3,
     b = 3. * (p0 - 2.*p1 + p2),
     c = 3. * (p1 - p0),
     d = p0 - p;

Then we can find the y-roots and check every point on the x-axis. For every crossing point (at most 3), we switch the sign:

    float r[5];
    int count = root_find3(r, a.y, b.y, c.y, d.y);
    vec3 t = vec3(r[0], r[1], r[2]);
    vec3 v = ((a.x*t + b.x)*t + c.x)*t + d.x;
    if (count > 0 && v.x >= 0.) w += inc;
    if (count > 1 && v.y >= 0.) w -= inc;
    if (count > 2 && v.z >= 0.) w += inc;

Since we already have a 5th degree root finder from the previous article, we just have to build a tiny version for the 3rd degree:

int root_find3(out float r[5], float a, float b, float c, float d) {
    float r2[5];
    int n = root_find2(r2, 3.*a, b+b, c);
    return cy_find5(r, r2, n, 0., 0., a, b, c, d);
}

To summarize:

int bezier_winding(vec2 p, vec2 p0, vec2 p1, vec2 p2, vec2 p3) {
    int w = 0;
    int signs = int(p0.y < p.y)
              | int(p1.y < p.y) << 1
              | int(p2.y < p.y) << 2
              | int(p3.y < p.y) << 3;
    if (signs == 0 || signs == 15)
        return 0;
    int inc = (signs & 1) == 0 ? 1 : -1;
    vec2 a = -p0 + 3.*(p1 - p2) + p3,
         b = 3. * (p0 - 2.*p1 + p2),
         c = 3. * (p1 - p0),
         d = p0 - p;
    float r[5];
    int count = root_find3(r, a.y, b.y, c.y, d.y);
    vec3 t = vec3(r[0], r[1], r[2]);
    vec3 v = ((a.x*t + b.x)*t + c.x)*t + d.x;
    if (count > 0 && v.x >= 0.) w += inc;
    if (count > 1 && v.y >= 0.) w -= inc;
    if (count > 2 && v.z >= 0.) w += inc;
    return w;
}

For every sub-shape, we can accumulate the winding number, and use it at the end to decide whether we're inside or outside:

float get_distance(vec2 p, Bezier buf[N], int counts[NC]) {
    int w = 0;
    int base = 0;
    float dist = 1e38;

    for (int j = 0; j < NC; j++) {
        int count = counts[j];

        // Get the sign of the distance
        for (int i = 0; i < count; i++) {
            Bezier b = buf[base + i];
            w += bezier_winding(p, b.p0, b.p1, b.p2, b.p3);
        }

        // ...
    }

    // Positive outside, negative inside
    return (w != 0 ? -1. : 1.) * sqrt(dist);
}

And voilà:

Limitations

Wicked curves

This may look satisfying, but it's only the beginning of the problems. For example, variadic fonts are typically following chaotic patterns:

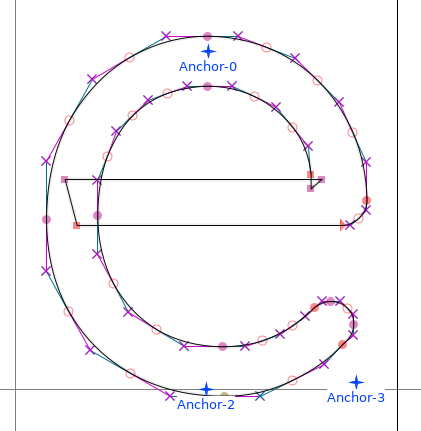
In addition to the self overlapping part, notice the reverse folding triangle on the right.

This completely wreck the distance field:

Even with a simple character display (meaning something that doesn't exploit the wide range of effects available with an SDF), it starts to glitch:

Little "cracks" should appears around the overlaps. This can be mitigated by lowering the distance by a tiny constant to avoid the zero-crossing, but it impacts the overall glyph (it gets more bold).

And it's not just because of variadic problem, sometimes designers rely on overlaps for simplicity:

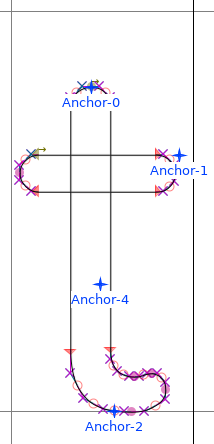
And sometimes... well let's say they have a legitimate reason to do it:

This is not something that can be addressed easily.

For example, take these two overlapping shapes:

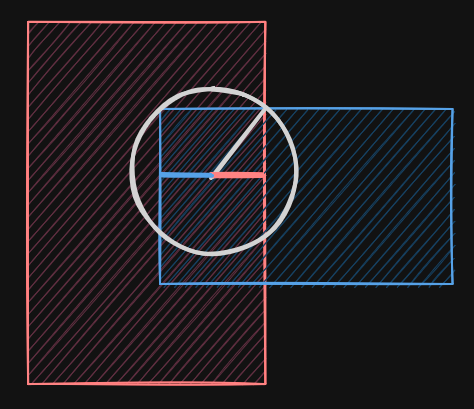
We see that the actual distance (white circle) is not the smallest distance to either shape, and it's not even the smallest distance to any edge: it is at an intersection point between two curves, which we do not have. Here we're dealing with line segments, but with cubic curves, the problem explodes in complexity.

At this point, we need another strategy, like feeding the GPU renderer with preprocessed outline-only curves. Many people rely on curves flattening to address this issue. This is unfortunately yet another field of research that we're not going to explore this time.

Inigo talked about the combination of signed distance if you want some ideas, but aside from the first one (giving up), none seems particularly applicable here.

Atlas and overlapping distances

Some effects such as blur or glow expand beyond the boundaries of the characters, so the distance field needs to be larger than the glyph itself. This means when an effect spread too large, there will be an overlap. If we're making an effect on a word, the distance field must be the unified version of all the word glyphs (or sometimes even the sentence). The classic approach of an atlas of glyph distances will not work reliably.

In the following illustration, a geometry per glyph is used, each geometry is enlarged to account for the larger distance field, and we end up with potential overlaps when applying effects.

Rounded corners

Like all distance maps, it suffers from the same limitations. The most common one is the rounded corners problem. This is typically addressed using a multi-channel signed distance field generator, but it's hard for me to tell how accessible it is for a portage on the GPU.

Effects

Despite all these limitations, we can already do so much, so let's close this article on a positive note. This is not done here, but all of these effects are free as soon as we have the distance field stored in an intermediate texture.

First, we have anti-aliasing / blur:

I wrote a dedicated article on the subject of AA (and blur) on SDF if you want more information on how to achieve that.

The shape can also be drastically altered with a simple operator such as "rounding":

d -= rounding;

This is the same technique we suggested to cover up for the overlap glitch earlier, just rebranded as an effect.

In the same spirit we can also create an outline stroke (on the outer edge to preserve the original glyph design):

This is sooo useful because it makes it possible for our text to be visible no matter what the background is. So many editors don't have this feature because it's hard and expensive to do correctly. Given a distance field though, all we have to do is this (which also includes anti-aliasing on every border):

float aa = fwidth(d); // pixel width estimates
float w = aa * .5; // half diffuse width
vec2 b = vec2(0,1)*outline - d; // inner and outer boundaries; vec2(-1,0) for inner, vec2(-.5,.5) for centered
float inner_mask = smoothstep(-w, w, b.x); // cut-off between the outline and the outside (whole shape w/ outline)
float outer_mask = smoothstep(-w, w, b.y); // cut-off between the fill color and the outline (whole shape w/o outline)
float outline_mask = outer_mask - inner_mask;
vec3 o = (inner_color*inner_mask + outline_color*outline_mask) * outer_mask;

We can also dig into our character with d = abs(d)-ring:

And maybe apply some glow to create a neon effect:

float glow_power = glow * exp(-max(d, 0.) * 10.);
o += glow_color * glow_power;

We could also do drop shadows, all sorts of distortions, or so many other creative way exploiting this distance. You get the idea: it is fundamental as soon as you want fast visual effects.

Conclusion

This article is the last of the series on 2D rendering for me. I've wanted to share this experience and knowledge after many years of struggling (mostly alone) on these issues. I wish I could have succeeded in providing a good free and open-source text effects rendering engine to compete with the industry standards. (Un)fortunately for me, the adventure stops here, but I hope this will benefit creators and future tinkerers interested in the subject.