From roots to polynomials

Polynomials can be represented in various forms. The most common ones are those I call the "sum of powers" (for example f(x)=ax³+bx²+cx+d) and the "root factors" (for example f(x)=(x-r)(x-s)(x-t), where r, s and t are the roots). The process of transforming the former into the latter is called "root solving"; the goal is to find all the x that satisfy f(x)=0. This is a field of research that has been going on for hundreds of years. But what about the reverse operation?

Roots finding

Most of the literature circles around roots finding. Analytic solutions to obtain these roots exist up to degree 4 (f(x)=ax⁴+bx³+cx²+dx+e), and at each degree the complexity increases dramatically. Starting degree 5 it is proven that no analytical solution can exist and we must rely on trial and error methods.

It is interesting to note that even though we've known how to find these roots mathematically for about 500 years, it is still a huge challenge for computers, mainly because of the arithmetic instabilities when working with IEEE 754 floating points. Aside from the multiple analytic solutions, many algorithms continue to appear to this day to address these shortcomings, with mixed results.

In order to evaluate these algorithms, I need to build polynomials in their "sum of powers" form using generated/known roots. More on that particular project in a future blog post, but the point is that the automation of the inverse operation is essential.

Roots concealing

If we were to transform the degree 4 polynomial f(x)=(x-r)(x-s)(x-t)(x-u) into f(x)=ax⁴+bx³+cx²+dx+e, we could just do it manually with basic arithmetic. It's a bit laborious, but there is nothing really difficult about it. But can we find a generic way of doing this transformation, for all degrees?

Since I'm a lazy engineer, my first reflex is to submit a 2nd degree polynomial to Wolfram|Alpha:

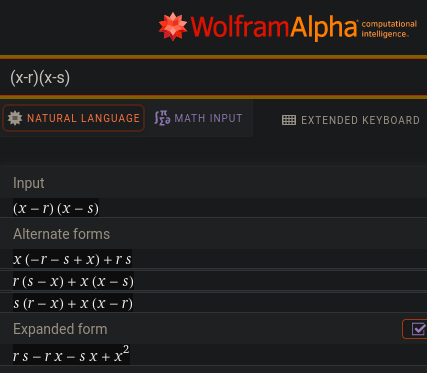
So for (x-r)(x-s) we get the expanded form: rs - rx - sx + x²

How about higher degrees?

• (x-r)(x-s)(x-t) gives -rst + rsx + rtx - rx² + stx - sx² - tx² + x³
• (x-r)(x-s)(x-t)(x-u) gives rstu - rstx - rsux + rsx² - rtux + rtx² + rux² - rx³ - stux + stx² + sux² - sx³ + tux² - tx³ - ux³ + x⁴

If we group the powers properly, we get:

• degree 2: x² - (r+s)x + rs
• degree 3: x³ - (r+s+t)x² + (rs+rt+st)x - rst
• degree 4: x⁴ - (r+s+t+u)x³ + (rs+rt+ru+st+su+tu)x² - (rst+rsu+rtu+stu)x + rstu

It looks like a pattern is emerging! Some observations:

1. The first coefficient is always 1: technically it could be anything, but that anything would need to multiply every other coefficients. The polynomial wouldn't be the same, but the solutions would remain identical. This constant would act as some sort of scale on the curve, but it would always cross 0 on the same x values. We will keep 1 for now.
2. The signs alternate between - and +, starting with +
3. The 2nd coefficient is always the sum of all the roots
4. The last coefficient is always the product of all the roots

If we focus on the more complex coefficients, we see that they're always a sum of products of combinations of roots.

Let's see if we can figure out something with the help of the itertools module in Python. Can we for example rebuild the expression rst+rsu+rtu+stu (from degree 4) using rstu as input?

>>> from itertools import combinations
>>> list(combinations("rstu", 3))
[('r', 's', 't'), ('r', 's', 'u'), ('r', 't', 'u'), ('s', 't', 'u')]
>>>

It looks like we can. Hell, the product are even ordered the same (not that it matters). How about the rs+rt+ru+st+su+tu in the same degree?

>>> list(combinations("rstu", 2))
[('r', 's'), ('r', 't'), ('r', 'u'), ('s', 't'), ('s', 'u'), ('t', 'u')]

Similarly, we confirm that it works with 1 and 4 (2nd and last coefficient) and even the first coefficient. So for degree 4, the coefficients can trivially be obtained from:

• a: combinations("rstu", 0) (this is empty so involving no root, and thus leading to 1)
• b: combinations("rstu", 1)
• c: combinations("rstu", 2)
• d: combinations("rstu", 3)

More tests also confirm that this works the same for lower (and higher!) degrees.

Magic formula

In the end, we can build a very simple function:

from itertools import combinations
from math import prod

def coeffs_from_roots(roots):
    return [
        (1, -1)[i & 1] * sum(map(prod, combinations(roots, i)))
        for i in range(len(roots) + 1)
    ]

• (1, -1)[i & 1] gives us the +/- juggling; it can be replaced with -1 if i & 1 else 1, 1-(i&1)*2 or even (-1)**i
• sum(map(prod, comb...)) as the name implies is the sum of the products of the combinations

Edit: thanks to @raymondh for the suggested simplifications. Following this last link will give yet another improvement with regard to the sign handling.

Proof?

Let's be clear, I have absolutely no proof that this will work for all degrees, it was only inferred from observation. Instinctively, it looks pretty reliable to me, but if someone knows a proof for this, don't hesitate to contact me. Edit: apparently, these are Vieta's formulas, thanks jix!

I'd be very happy to hear if there is a named theorem and demonstration out there about this particular property. I'm also curious about how the function I wrote in Python would look like in a mathematical notation. I know the sum and product symbols, but I'm not sure how the combination would be expressed.